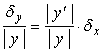§2.8 微分在近似计算中的应用

一、几个近似计算公式

设函数在处的导数，且充分小时，有

这里：，

故有如下近似公式

(1)

(2)

(3)

(1)、(2)、(3)式在近似计算中的作用：

若，容易计算时，那未

(1)式可用于近似计算函数在处的增量。

(2)式可用于近似计算函数在附近的函数值。

(3)式表明： 只要充分接近，函数可用线性函数

来替代。

用(2)、(3)式来作近似计算，关键是选择点，的选取标准有两条：

1、、易于计算。

2、 或 尽可能地小。

【例1】有一批半径为1厘米的球， 为了提高球面光洁度，要镀上一层铜，厚度定为0.01厘米，试估计每只球需用多少克铜(铜的比重是)?

解：镀铜前的球半径为=1 (厘米)

镀铜后球的半径的增量为 =0.01 (厘米)

而球的体积公式是 ，， 这里是球的半径。

镀铜层的体积为

每只球的需铜量约为 。

【例2】求 的近似值

解：将化为弧度

这里取函数为 ，，

由近似公式(2)计算函数 的近似值

注：值的计算可在MATLAB中键入表达式

sin(pi/6)+cos(pi/6)*(pi/360)

然后将结果粘贴到此。

二、几个工程中常用的近似公式

在(3)式中，取时，形式变为 (充分小)

利用此式， 可以得到几个工程中常用的近似计算公式。

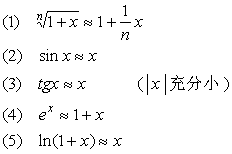
这些公式的证明较容易，仅证第(5)式，其余的留给同学们自行验证。

取，，

【例3】计算 的近似值。

解：

由近似公式(1)有：

三、微分用于误差估计

1、误差估计中的几个概念

设某个量的精确值为，它的近似值为，则称为的绝对误差。

而比值称为的相对误差。

一般说来，某个量的精确值往往是无法知道的，于是绝对误差和相对误差就无法求得。因此，在误差估计中， 常常是确定误差的范围。

若 ，则 称为测量的绝对误差限；

而比值 称为测量的相对误差限。

【例4】测得圆钢截面的直径，测量的绝对误差限为
。若利用公式计算圆钢的截面积，试估计面积
的误差限。

解：将测量时所产生的误差当作自变量的增量，

利用计算时的误差可看作函数的对应增量，

当充分小时，可以用近似代替，

即

而的绝对误差限为毫米，即：

从而：

故的绝对误差限为

的相对误差限为

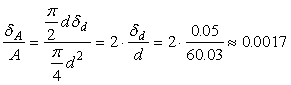
2、误差限的计算公式

仿上例，可给出利用测量值，按公式计算值时，其误差限的确定公式。

设测量的误差限为，即： ，当 时，

有 ，

的绝对误差限为：

的相对误差限为：